初级魔法使指南-滤波器设计入门(上)

0-引言

这次我们来讲讲模拟滤波器设计，from DC to Light~(0Hz to THz~)。

由于篇幅过长，我想将这篇文分成上中下-共三篇写完。这篇主要是介绍滤波器的数学原型和基本参数，下一篇我们讨论讨论从低频集总滤波器到微波段的分布式滤波器的转换，以及网络综合理论。结尾篇我们讲讲滤波器的工程应用中如何取舍平衡参数，以及介绍一些高级滤波器技术。

同样的，这个系列文章中有很多内容是和 射频微波入门指南 这篇文高度重合的。由于这个坑挖的太大，一时半会儿我还填不上，所以想着把部分小章节拆出来单列文章，这样至少能保证写得下去…目标设的太大最后就容易鸽了，233。

1-理论基础

1.1-滤波器基本类型

一般滤波器按照 通带(Pass-Band)特性 可分为5种，分别是：

低通滤波器（Low-Pass Filter，LPF）
高通滤波器（High-Pass Filter，HPF）
带通滤波器（Band-Pass Filter，BPF）
带阻滤波器（Band-Stop Filter，BSF）
全通滤波器（All-Pass Filter，APF）

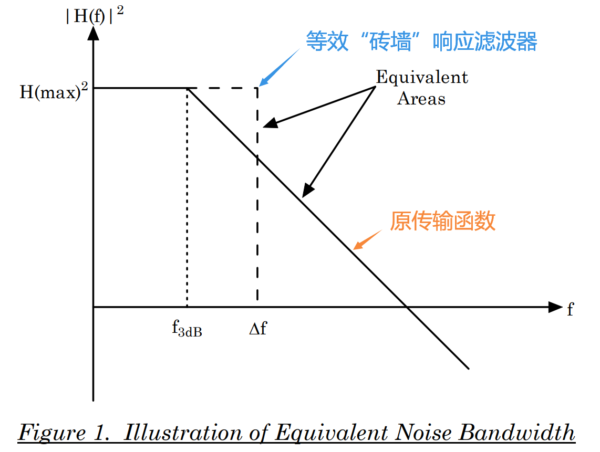
理想滤波器的响应如下图。当然，理想滤波器的通带和阻带之间的过渡带是无限窄的，被称为 "砖墙式(Brick-Wall)" 响应，这种响应在现实中是不可能实现的，只用于理想模型描述。

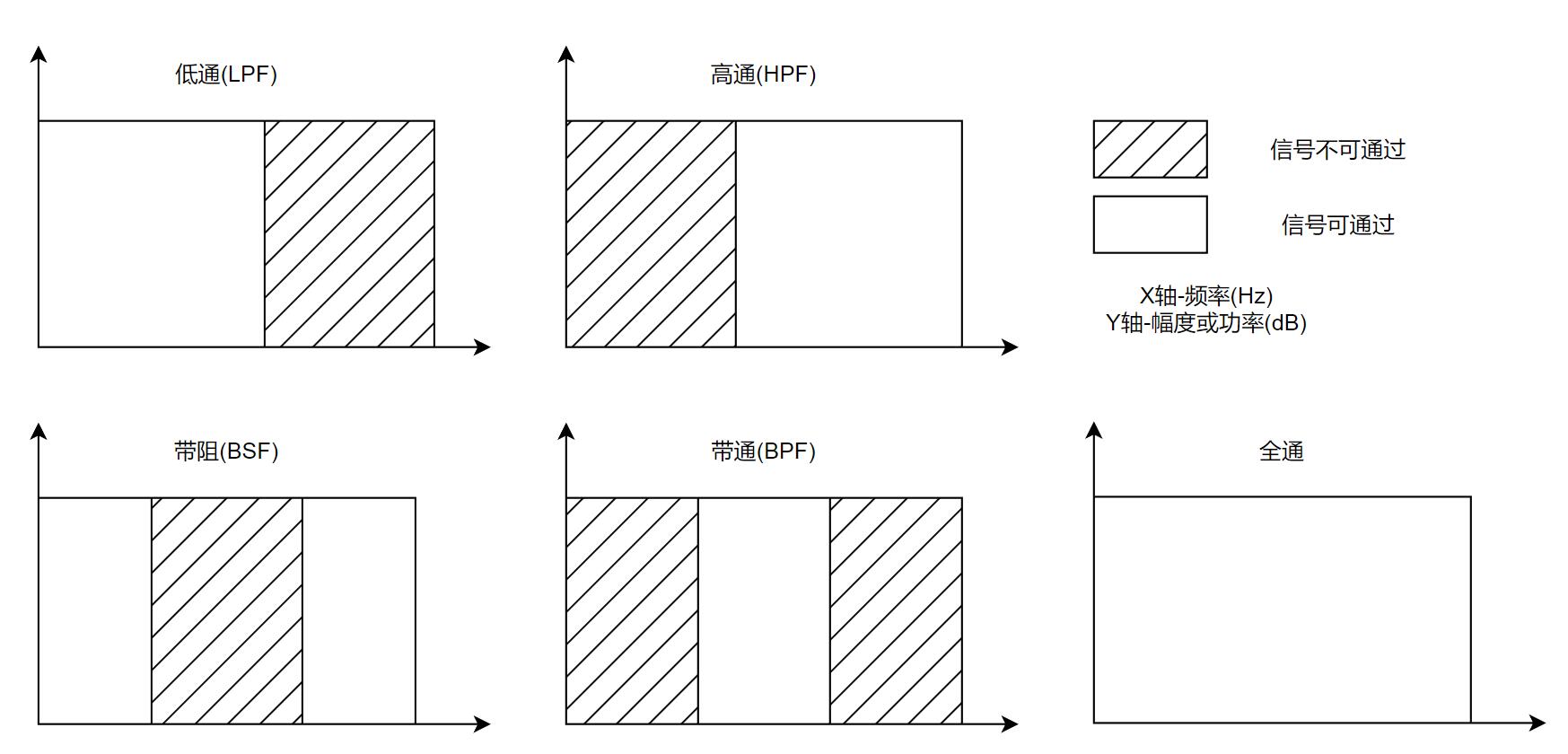
当然，特殊应用场景下，还存在多通带滤波器(Multi-Band)，它相当于是一个具有多个通带的带通滤波器，比如2.4GHz/5.8GHz蓝牙/Wi-Fi链路中可能就会用到这种滤波器。有多通带就有多阻带，但本文不讨论这些。

从滤波器的 系统函数 出发，也可以将滤波器分为以下几种基本响应型(Response Type):

巴特沃斯（Butterworth）
切比雪夫（Chebyshev）(有Ⅰ型和Ⅱ型)
贝塞尔（Bessel）
椭圆/考尔（Elliptic，或Cauer）
…

上述4种最常见也最标准，此处不引申别的类型(如高斯，最平坦等)了。
巴特沃斯型具有最平坦的通带，其特征是在截止频率处，衰减（插损）为3dB，这也是Butterworth的特征之一。
切比雪夫型具有最陡峭的过渡带（滚降(roll-off) 快），但是通带内有隆起（Ripple）
贝塞尔型滚降最缓慢，但是其具有最大线性相移区间（通带群延迟平坦），可减小复合波形的相位失真，这一点在宽带通信系统中尤为重要。

滚降(Roll-Off)是个很形象的词，描述了滤波器从通带过渡到阻带时，幅频特性曲线下降的快慢，简单来说就是斜率~斜率的绝对值越大（越陡峭），滚降越快，反之亦然。

椭圆滤波器具有零点（前三种只有极点（Poles），没有零点（Zeros）），椭圆滤波器具有最快的滚降（最窄的过渡带），但是其通带和阻带内都有波动；偶数阶的阻带增益很小但不会随频率增大而趋近于0，奇数阶的阻带随着频率增加趋近于0，所以工程应用上奇数阶应用更多一些~

1.2-系统函数

待补充。

1.3-零极点

待补充。

1.4-归一化(Normalize)

在设计和分析滤波器时，我们经常需要对比不同频段和带宽的滤波器性能，但是直接用实际频率去对比会比较麻烦，因为每次都要将相对频率转换运算。这时我们不妨借助归一化思想，将滤波器的 频率归一化 到一个统一的标度上进行对比。

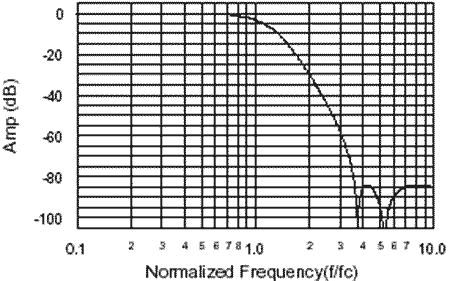
如上图所示，该滤波器的截止频率被归一化到1(Hz)，它可以代表具有这种响应的一族滤波器，只需要将频率乘以想要的目标截止频率，就能得到一个具有这种响应的、全新的滤波器。在后面的设计滤波器环节，归一化也得到了充分的应用。

2-滤波器重要参数

2.0-衰减/插损/抑制-术语辨析

这三个词经常混着用，不同的工程师有不同的说法。但其实理解了意思之后，还是很容易理解的。

衰减(Attenuation):某频点处,输出信号相对于原值衰减的比例，单位有时是数值，有时是dB，适用于所有描述滤波器的语境
插损(插入损耗,Insertion Loss,简写IL):定义为某频率处的衰减值，一般单位是dB，该词多用于射频系统中
抑制(Suppresion):一般用于描述滤波器在阻带某频率处的衰减大小。(通带就不能说"抑制"了…)

我们拿一个具体的低通滤波器举例，来说明这3个词怎么用。

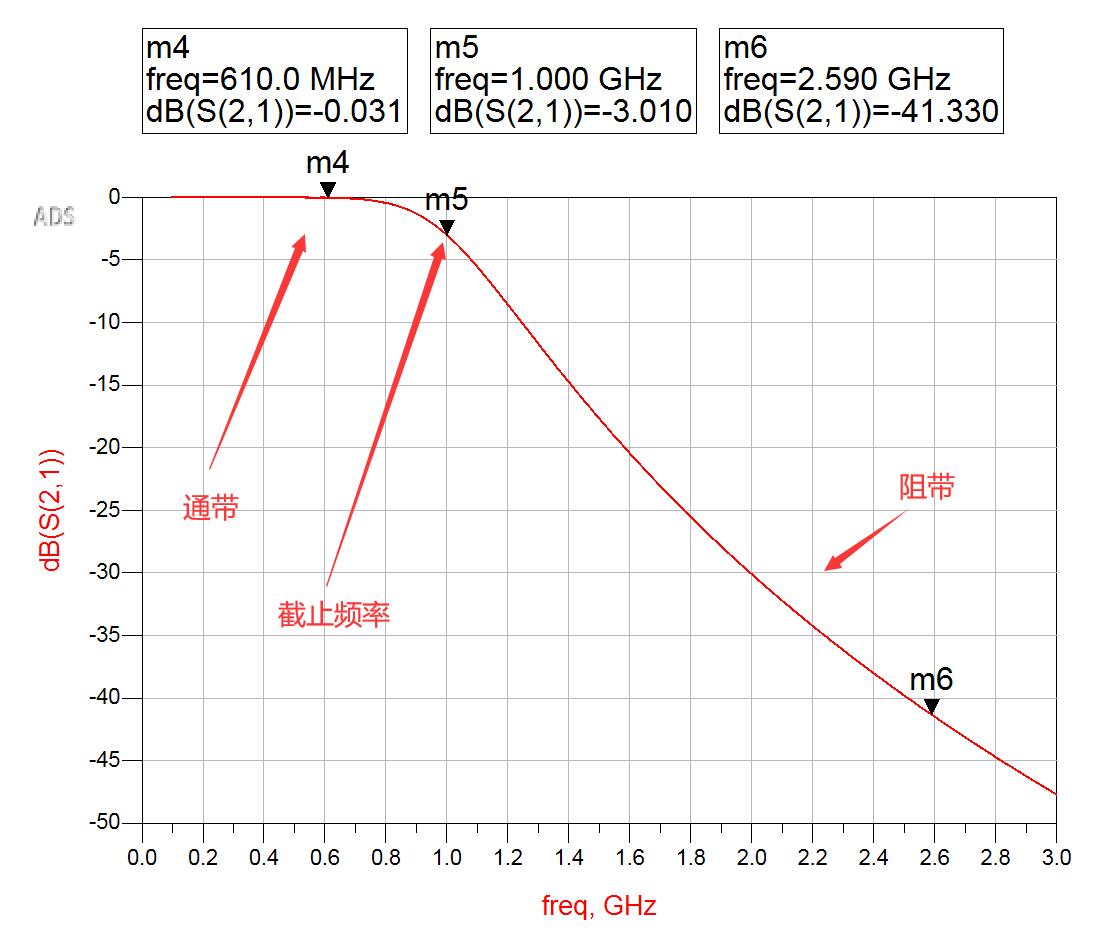
这是一个5阶巴特沃斯响应的低通滤波器。其在610MHz处的插损/衰减(此处不说抑制)为0.031dB(由于是衰减，不说负号。但其实没那么死板，因为你说衰减/插损别人就明白是啥意思了…除非你的滤波器是有源的，在通带内有增益。)
在截止频率(1GHz)处的插损/衰减为3.01dB，在2.59GHz处的抑制为-41.33dB(插损/衰减为41.33dB)。

2.1-幅度特性-通带/阻带的衰减特性

可能你已经注意到理想滤波器与实际滤波器的区别了。我们以一个实际的低通滤波器为例，来看看下面这张图：

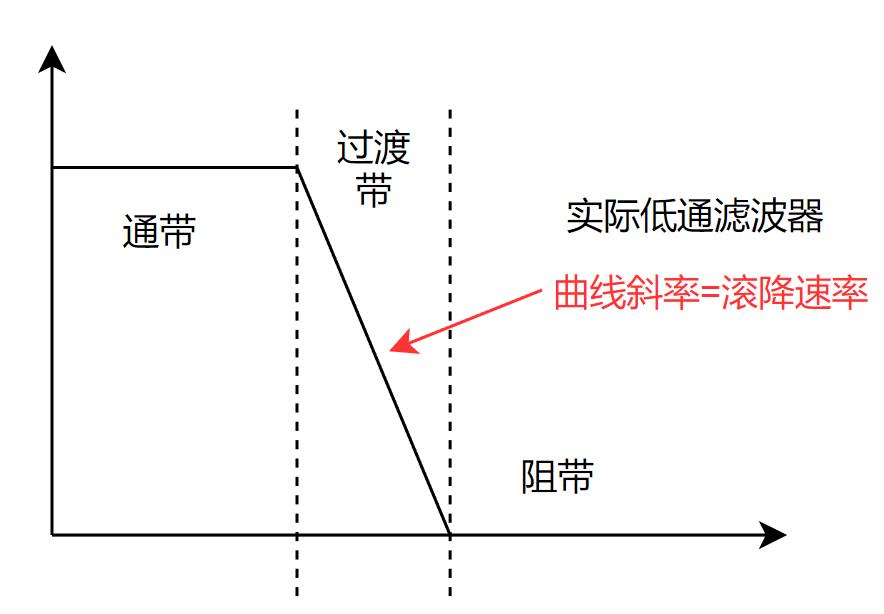
理想滤波器的响应是砖墙式的，即不存在过渡带(或者过渡带无限窄)，通带之外的频带全是阻带。当然这是不可能的，诸多物理因素限制了滤波器的极限，包括但不限于:

滤波器结构前后的空间电磁场耦合,导致抑制性能下降
电路中的热噪声,限制了滤波器衰减的下限
构成滤波器的元器件的非理想参数,在抑制带形成寄生通带
……

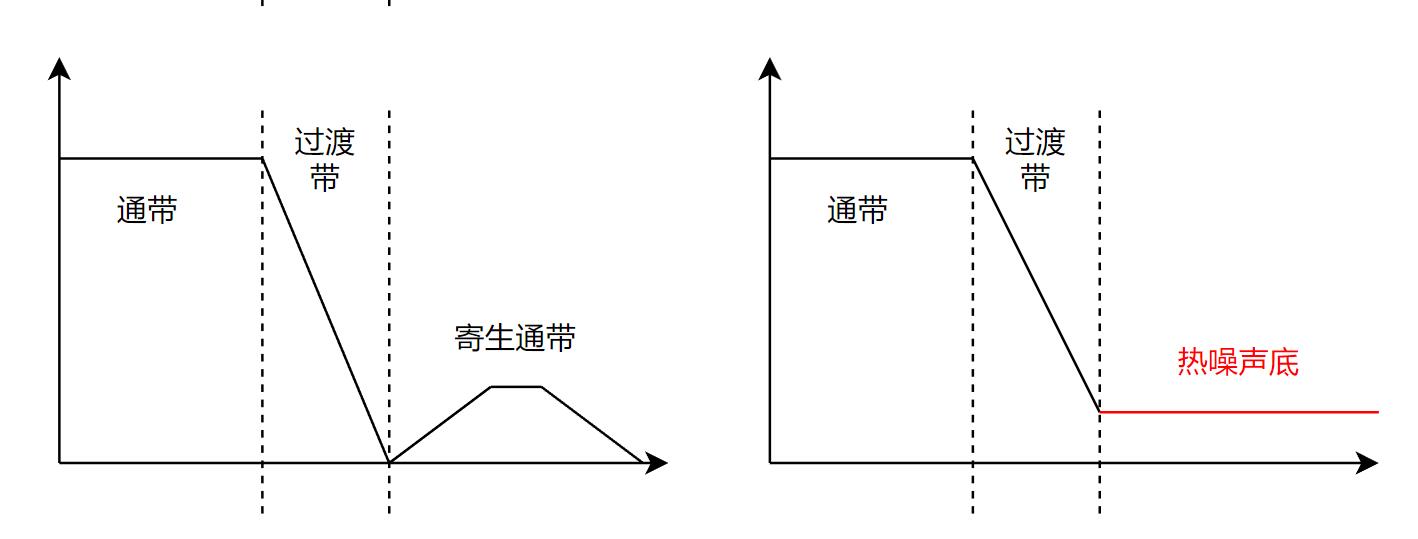
(well…上面的图中，我没有标注y轴的幅度，所以这些图仅供示意。)

2.1.1-纹波(Ripple)

取决于滤波器的响应型，滤波器的通带和阻带特性也并不一定是一条毫无起伏的直线。
如下图所示，如果说巴特沃斯是光滑与柔顺的代表，那切比雪夫和椭圆响应型就是其对立面。其中，切比雪夫Ⅰ型响应在通带中存在纹波起伏，但是其阻带中没有；切比雪夫Ⅱ型响应在阻带中存在纹波起伏，但是其通带中就如同巴特沃斯一样，十分光滑。椭圆则是在通带和阻带中都存在纹波起伏，但是椭圆的过渡带滚降是最快的。这就像其他电路设计一样，不存在一个处处完美的解决方案。最平坦&快滚降这两者不可得兼，有失必有得- -。

2.1.2-截止频率/衰减定义

2.1.2-Q值

2.2-幅度特性-滚降速率

我们可以使用Keysight的ECAD工具——ADS(Advanced Design System)来观察一下不同响应型滤波器的特性。首先抓出4种基本响应型的低通滤波器的理想模型，将他们的参数都配置成5阶，截止频率1GHz。

加上源和终端电阻，设置S参数扫描，得到4个幅频特性曲线如下(S21):

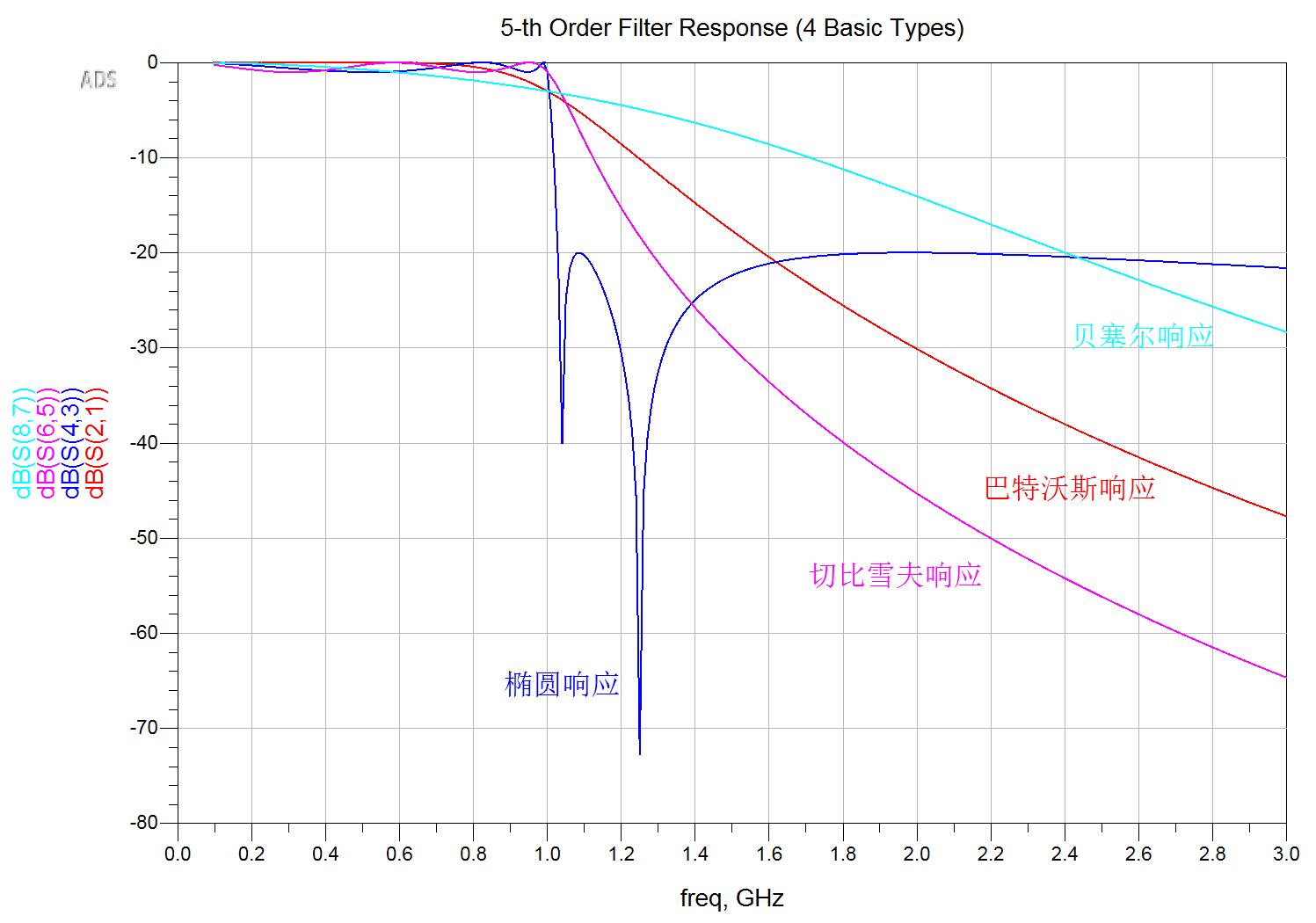
不难看出，在同等阶数，相同截止频率的条件下，过渡带（LPF的截止频率处,频率增加的方向）最陡峭的当属椭圆响应。滚降速率排序从高到低为：椭圆>切比雪夫>巴特沃斯>贝塞尔。

2.2.1-估算所需滤波器的阶数

滤波器的阶数越高，其滚降就越快;那么阶数和滚降速率是否有对应关系呢？在信号与系统中能找到这个问题的答案。

2.2.1.1-一阶RC系统

以最简单的1阶RC低通滤波器为例，其传递函数为：

 $H(s) = {RCs \over 1+RCs}$

该传输函数在 $s=-{1 \over RC}$ 处有一极点。一阶RC系统的幅度为：

 $|H(\jmath\omega)| = {1 \over \sqrt{1+(\omega RC)^2}}$

将频率变换到 $\omega_c=1/RC=1$ ，同时将幅度变换成功率：

 $|A|^2={1\over 1+({\omega \over \omega_c})^2} = {1\over 1+\omega^2}$

转换成对数，并用插损表达:

 $Insertion \ Loss(IL) = 10\log(1+\omega^2) \ (dB)$

在频率远大于 $\omega=1$ 处，上式简化为：

 $Insertion \ Loss(IL) = 10\log(\omega^2)=20\log(\omega) \ (dB)$

于是，在阻带的2个频点处，其中的插损滚降为：

 $\Delta L = 20\log ({\omega_2 \over \omega_1}) \ dB/interval_{2,1}$

在一个一阶RC系统的阻带中，对于10倍频程(decade)来说，每10倍频程的滚降就是20dB；对于2倍频程(octave)来说，每2倍频程的滚降就是6dB。比如下图中的fc处，插损为3dB，那么频率到2*fc处时，插损就是3+6=9dB，10倍fc处时，插损就是3+20=23dB。

2.2.1.2-具体到滤波器响应型

实际上，上述的一阶RC系统响应，就是巴特沃斯响应型滤波器的特征。

然而这个滚降速率的估计方法并不适用于所有滤波器结构。它只是从最简单的一阶RC低通滤波器传输函数出发推导而来的一个估计方法，具体到每个不同响应型的滤波器，其传输函数将发生变化，该推论不一定适用，只能作为参考评估。

不过既然此方法是基于巴特沃斯响应型滤波器去评估的，而我们又知道贝塞尔的滚降比他慢，切比雪夫和椭圆的滚降比他快，那我们至少可以在设计滤波器时，参照这个标准来预估滤波器的抑制性能。

2.2.2-N阶低通滤波器滚降计算

N阶滤波器可以由多节单阶滤波器级联而成，如果各阶滤波器前后输入输出匹配，在理想情况下N阶滤波器的滚降速率为：

 $\Delta L = N\cdot 20dB \ per \ decade(10倍频程) \\ \Delta L = N\cdot 6dB \ per \ octave(2倍频程)$

例如一个1GHz截止频率的5阶巴特沃斯低通滤波器，其在2GHz处的衰减理论上来说应该为 6×5 = 30dB（理想滤波器）。下图的仿真模型也很好地确认了这一点(Mark2处标记2GHz处的衰减，刚好是30.0dB左右)。

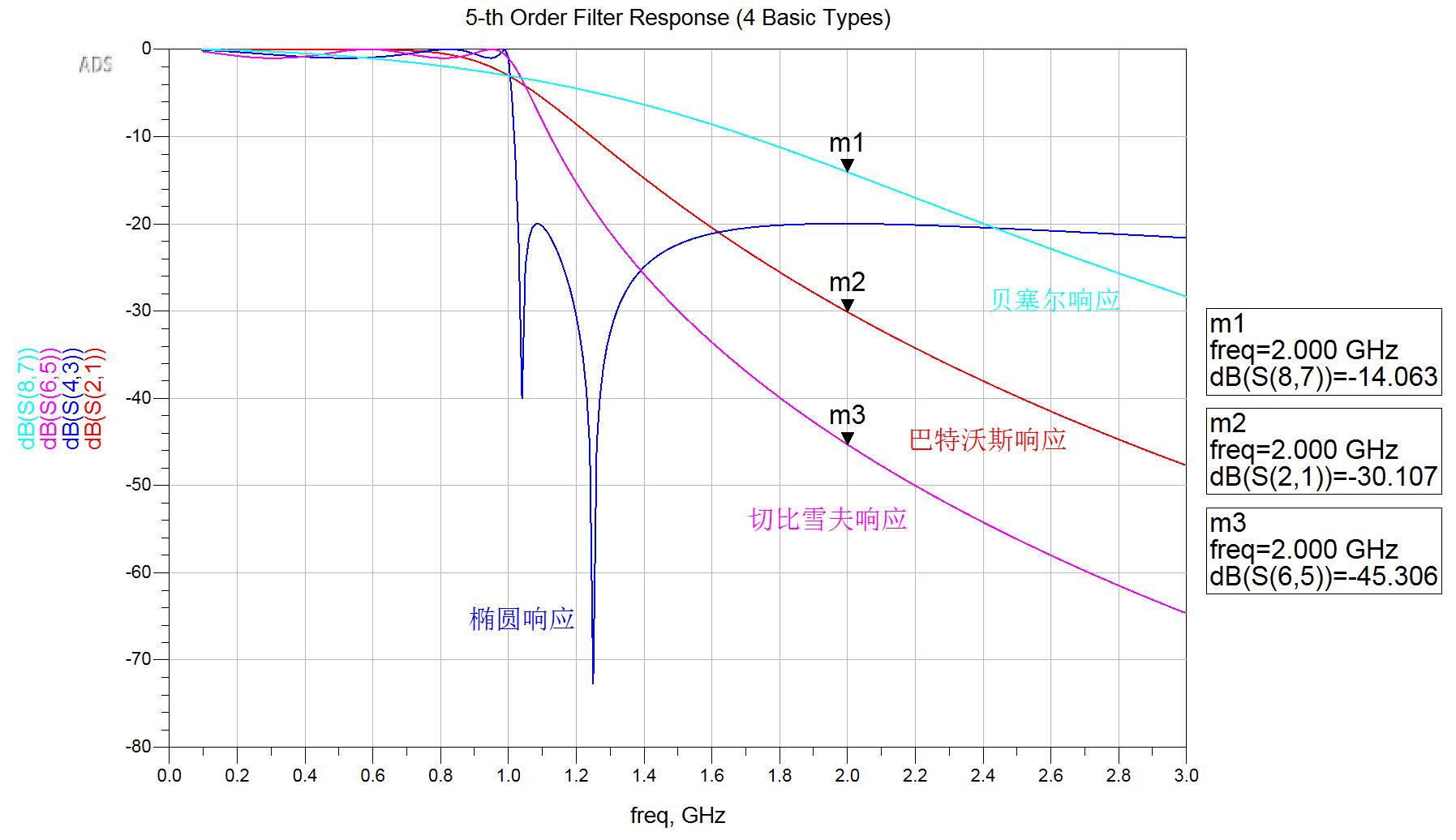
同时我们也能看出切比雪夫和贝塞尔相对于巴特沃斯，在2GHz处的衰减值相对于巴特沃斯型，各有15dB左右的差值。

2.2.3-更通用的估算公式

参考该滚降公式，对于巴特沃斯型低通滤波器，可以得出距离截止频率任意频率处的滚降。(1为截止频率，2为待计算频率)

 $\Delta L = N \cdot 20\log({f_2\over f_1}) \ dB/interval_{2,1}$

如果转换到带通滤波器，现在则需要考察其特征中心频率 $f_0$ 和通带带宽 $f_{BW}$ 。计算带通滤波器的阻带滚降速率所使用的频率基准不再是特征中心频率 $f_0$ ，而是通带带宽 $f_{BW}$ 的一半。
例如，一个通带中心频率为10GHz，带宽为1GHz的7阶巴特沃斯带通滤波器,其通频带为9.5GHz~10.5GHz，那么他的特征中心频率 $f_0$ 为:

 $f_0 = \sqrt{(10GHz-1GHz/2)(10GHz+1GHz/2)} = 9.9875GHz$

请注意，带通滤波器的 通带中心频率 和 特征(中心)频率 不等同！前者是2个过渡带边缘点的算术平均值，后者是几何平均值。

对于理想带通滤波器，上面的低通估计式稍作变化(0为特征中心频率,1为通带外的任意频率)：

 $\Delta L = N \cdot 20\log({|f_1-f_0| \over f_{BW}/2}) \ dB/interval_{1,0}$

如同上述举例中的一个中心频率为10GHz，带宽为1GHz的7阶理想巴特沃斯带通滤波器，其通频带为9.5GHz~10.5GHz，则下列频率处的衰减理论值约为：

 $\Delta L_{10.8GHz} = 7 \cdot 20 \log({ 10.8GHz-9.9875GHz \over 1GHz/2 }) \ dB = 29.52dB \\ \Delta L_{11GHz} = 7 \cdot 20 \log({ 11GHz-9.9875GHz \over 1GHz/2 }) \ dB = 42.90dB \\ \Delta L_{13GHz} = 7 \cdot 20 \log({ 13GHz-9.9875GHz \over 1GHz/2 }) \ dB = 109.19dB \\ \Delta L_{7GHz} = 7 \cdot 20 \log({ |7GHz-9.9875GHz| \over 1GHz/2 }) \ dB = 108.69dB \\$

最后请记住，上述结论 只适用于估算巴特沃斯响应型的滤波器滚降。

2.3-相位特性-群延迟

当然，除了幅度响应之外，相位响应也是我们关心的。通常用 群延迟(Group Delay) 来评价一个系统的相位特性。当信号通过滤波器时，会发生相位移动，对于不同的频率成分，相移的大小也不一样。群延迟这一指标就是 某一频率下，系统产生的相移对该频率的导数，严格的数学定义在此不给出;不过管中窥豹也可知其一二：如果某个系统的群延迟在所有频率处恒定，说明一个含有多种频率成分的信号通过该系统后，各频率成分信号的相位关系不发生改变，即 在时域中，此信号进去长什么样，出来还是什么样。

上述4种基本响应滤波器的群延迟特性如下，可以明显看出，椭圆滤波器不太适合用来处理复合波形，它的群延迟在通带内突起太高了。但是在只需要单频信号且不考虑相位的系统中，椭圆是个香饽饽。贝塞尔响应的群延迟在通带内几乎是平坦的，这意味着即使Bessel的抑制性能不佳，但相位特性非常不错。

我们还可以通过时域仿真进一步确认这一点。设置一个125MHz基频的数字码型信号，分别通过截止频率相同、阶数相同的Bessel滤波器和切比雪夫滤波器，观察他们的输出波形长什么样，以及通过眼图说明其信号失真程度。

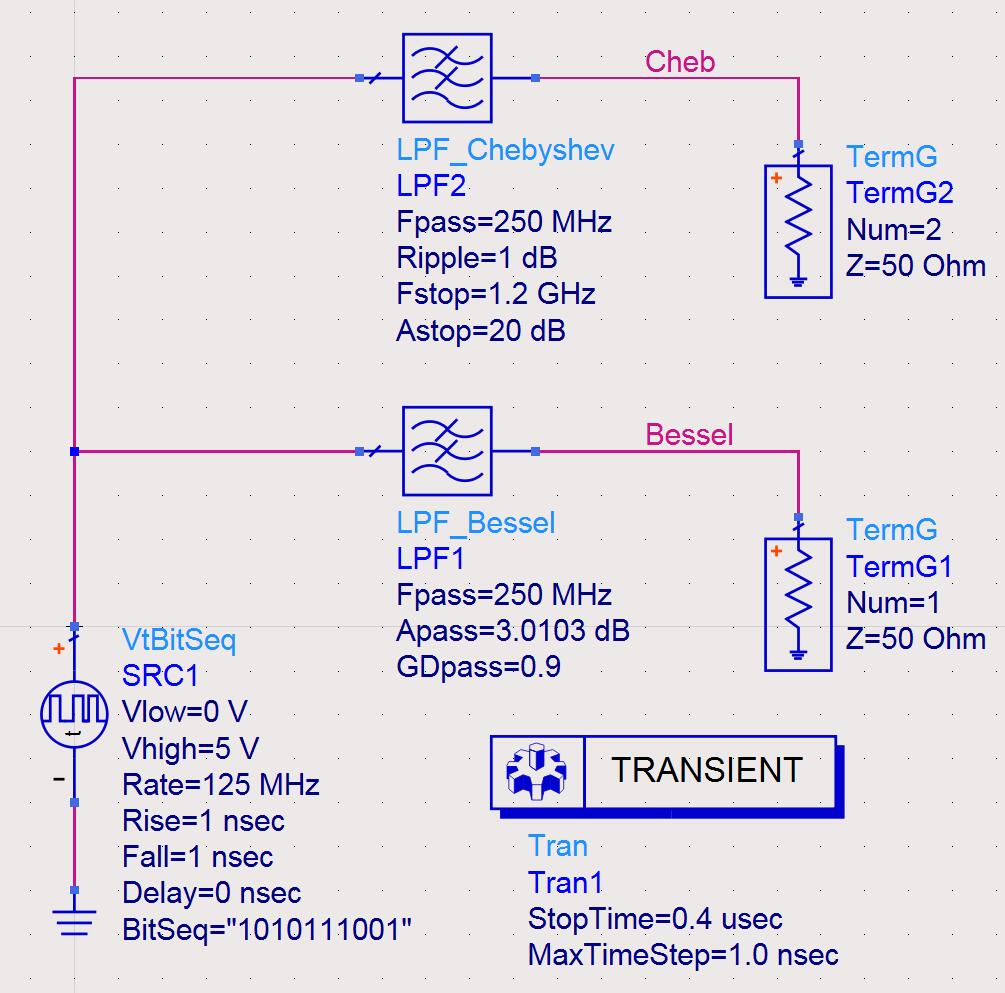
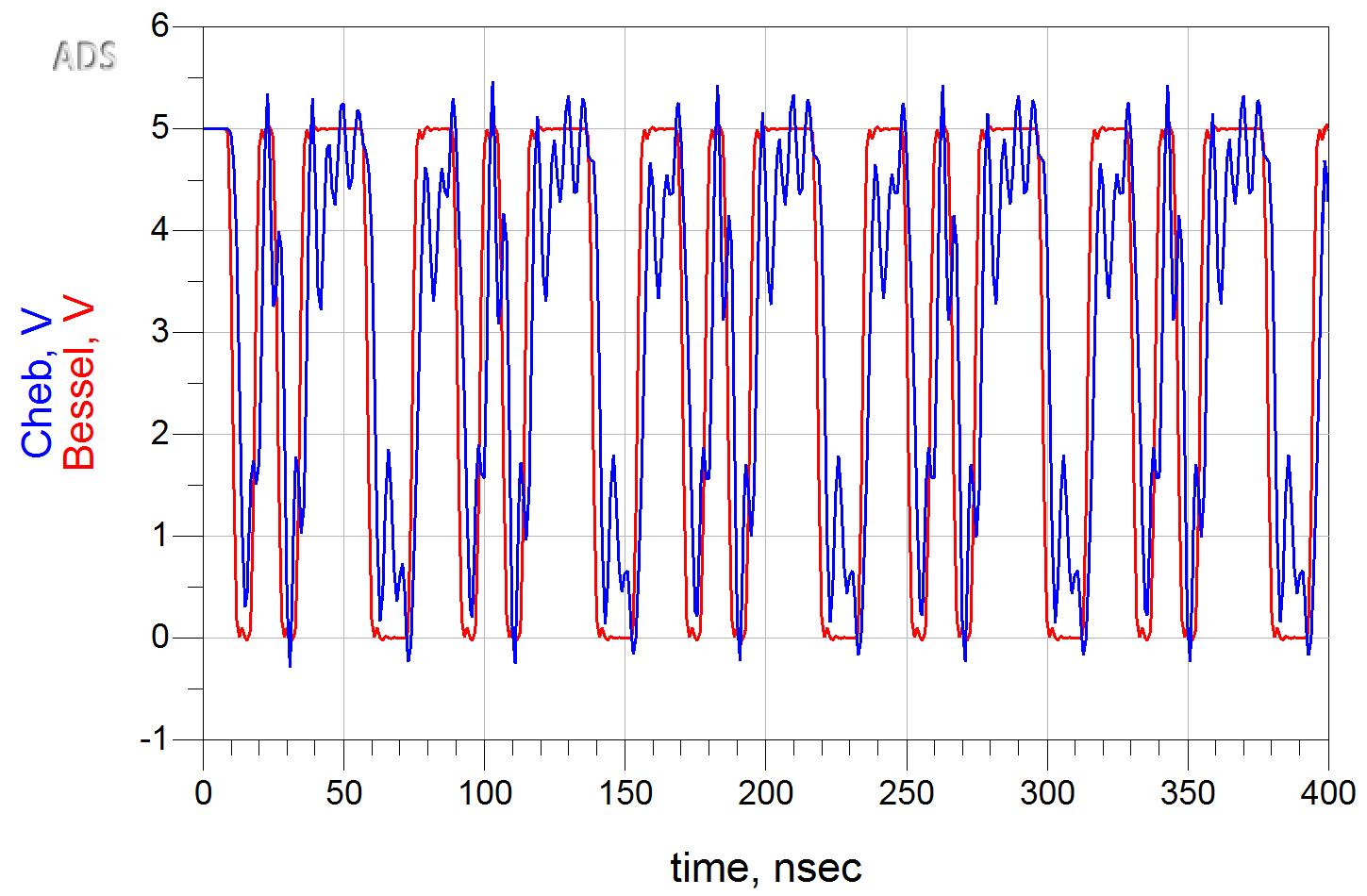
通过时域波形我们可以看出，通过Bessel滤波器的输出波形(红色曲线)基本维持了原波形形状，而通过Chebyshev滤波器的输出波形(蓝色波形)已经惨不忍睹…这是因为数字码流信号中包含从基频开始到很高次的谐波成分，这些谐波成分通过群延迟不平坦的切比雪夫滤波器时，发生了不均等的相移，造成了时域中的失真。

通过下面的眼图能更好地说明这点——左边是通过Chebyshev滤波器的眼图，右边是通过Bessel滤波器的眼图，高下立判了。(曲线间的空白区域越大，信号质量越高)