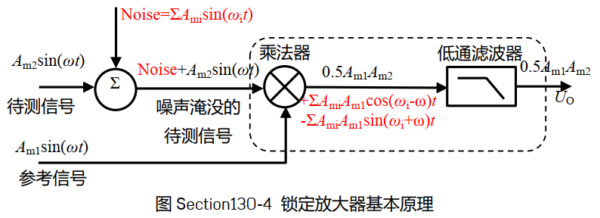
运算放大器噪声分析
在精密模拟电路设计中,噪声分析 是必不可少的。无论是使用无源器件如电阻电容等,还是有源器件如运算放大器、仪表放大器之类,噪声就像恼人的蚊子一样,始终盘旋在耳边。这次我们来讲讲运算放大器的噪声模型,以及分析方法。
之前🐟也写了有关噪声的3篇文章,分别是——
这3篇文章由浅入深、循序渐进地探讨了噪声对电路的影响,以及如何测量噪声。这次杀个回马枪,回归理论和魔电~
回顾热噪声
热噪声的学名叫 约翰逊-奈奎斯特噪声(Johnson-Nyquist Noise),也可称作约翰逊噪声、奈奎斯特噪声。热噪声是由于热搅动导致导体内部的电荷载体达到平衡状态时的电子噪声,与所施加的电压无关。
诚然,任何具有电阻的导体中都存在热噪声。一个理想电阻器的热噪声接近白噪声,其功率谱密度在整个频谱范围内几乎是不间断(连续)的(极高频时并未如此,不过这往往超出了中低频模拟电路的考虑范围)。限定噪声的带宽时,一个电阻的噪声等效模型如下所示,可等效为一个理想电阻串联一个交流噪声源。其热噪声的幅度近似为高斯分布。
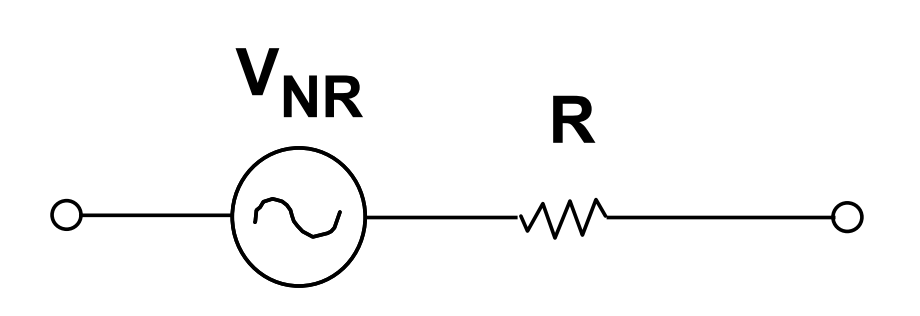
热噪声的单边功率谱密度由下式给出:
V_{Noise} = \sqrt{4kTR} \ \ (V/\sqrt{Hz})其中,T为绝对温度(摄氏度+273.15),k为玻尔兹曼常数(k=1.38*10^{-23} J/K),R是电阻的阻值。一个1kΩ电阻在25°C室温下产生的噪声谱密度是 4nV/\sqrt{Hz},记住这一点,对于快速计算很有帮助。
噪声谱密度要转换为实际电压值,需要对频率作积分。如果指定了计算的噪声带宽B的话,也可以直接使用下式计算出噪声电压真有效值:
V_{Noise} = \sqrt{4kTBR} \ \ (V)比如上面说过一个1k电阻的电压噪声谱密度是 4nV/\sqrt{Hz},如果我们计算的噪声带宽是10kHz,那么乘以 \sqrt{10^4}=100,就可以计算出一个1k电阻在10kHz带宽内产生的噪声电压真有效值为400nVrms。
超越噪声
可是很不幸的是,没有理想的元器件。实际生产的电阻器由于生产工艺、材料特性以及各种其他因素导致电阻器的噪声密度谱曲线并不是理想的一马平川(图中紫色曲线)。在极低频区域,电阻中也会存在1/f噪声,这些意料之外的多出来的噪声被视作 超越噪声。
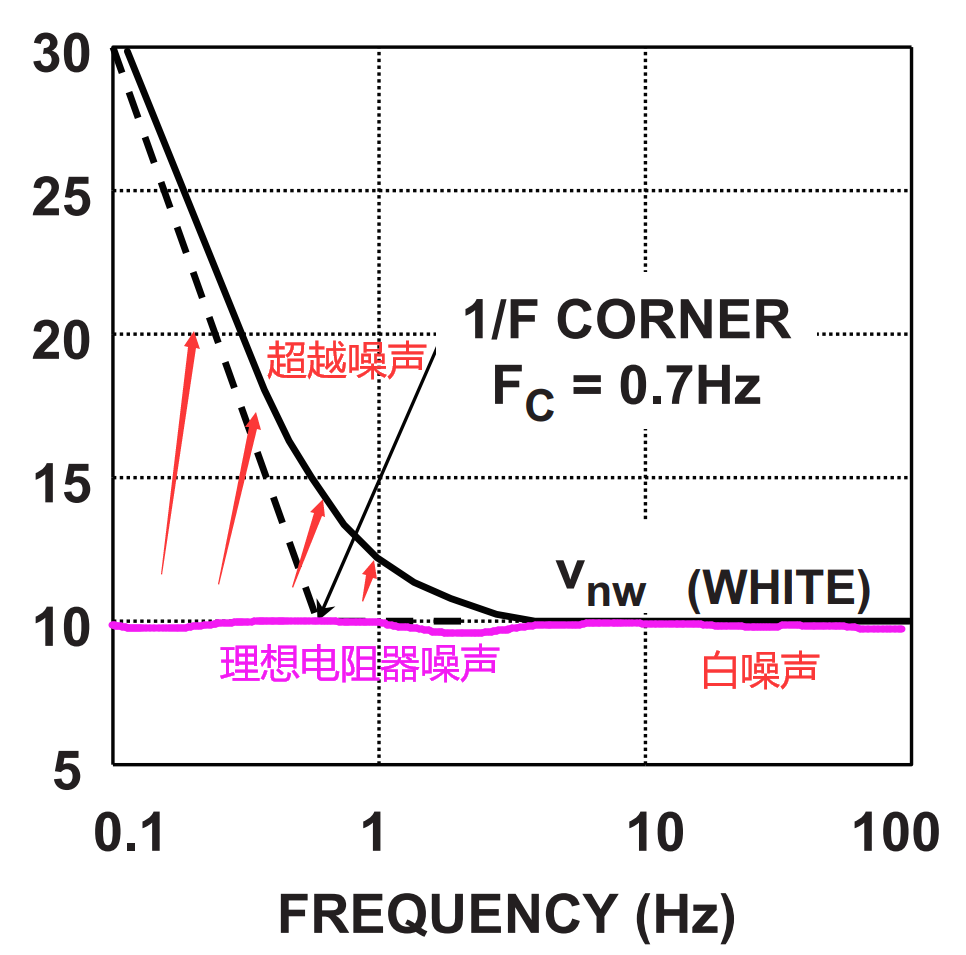
所以在实际计算电阻器为系统贡献的噪声时,采用理想白噪声模型实质上是最保守的估计。
运算放大器噪声源
我们一般说一个OpAmp的噪声,是指其内部产生的噪声,而不是因为外部电磁环境耦合进电路的噪声。虽然有时候系统的噪声性能取决于外部电磁环境耦合的程度,但我们就先假设运算放大器的最佳工作状态吧~
运算放大器内部是由晶体管、二极管与电阻、电容等元器件构建成的,有些特殊运算放大器会有其他的部件,在这里不予考虑。总的来说,OpAmp的噪声源可以在建模时等效为3个外部噪声源+理想无噪声运算放大器:
- 以差分形式出现在输入端的电压噪声源
- 输入端的电流噪声源
- OpAmp外围电阻的热噪声
我们逐一分析——
电压噪声
简单的电压噪声模型

OpAmp的输入电压噪声以噪声谱密度表示,单位通常是 nv/\sqrt{Hz}。这个参数通常会标注在器件的数据手册中,其大小因器件而异。通常所说的低噪声运算放大器的输入电压噪声密度在 10nV/\sqrt{Hz} 以下,最低的能做到 0.9nV/\sqrt{Hz}。而通用运放的噪声可能要大得多,10几甚至几十都是有可能的。但总的来说,现代OpAmp的电压噪声水平基本在这个数量级上,不会有很大的跨度。
双极性(BJT)输入级的运放电压噪声往往低于JFET输入级的运放,但其实他们的选择各有利弊,比如JFET输入级具有极高输入阻抗。在工程中这些往往需要权衡:)
电流噪声
简单的电流噪声模型

电流噪声的变化范围可就比电压噪声大很多了,甚至能跨数量级(图中所示的0.1fA至10pA)。数据手册中不一定会给出电流噪声值,但在简单的BJT或JFET等器件中却可以计算得出,因为在这类情况下,所有OpAmp输入偏置电流均流入输入结点,电流噪声就是偏置电流的肖特基噪声(或称散粒噪声)。
散粒噪声的噪声谱密度是 \sqrt{2I_B q} /\sqrt{Hz},其中 I_B表示放大器内的输入偏置电流,q表示电子电荷量(1.6*10^{-19}C)。不过在偏置补偿或电流反馈运算放大器中,外部偏置电流是两个内部电流之间的“差值”,因此无法计算出电流噪声。
只有在OpAmp的偏置电流有流动路径(比如流过接在输入端的电阻)时,才需要考虑电流噪声,因为此时电流噪声会在流过的阻抗上产生电压,等效转换为电压噪声。在运放的输入端保持相对较低的阻抗可以最小化电流噪声对系统噪声的贡献。但阻抗太小,输入电流会过大,所以也需要权衡设计~
合并上述噪声源
在合并前,我们需要了解一点计算规则。不相关的噪声电压以 方和根 的形式相加,当然对于功率来说,直接照常相加就好。比如说有均方根噪声电压 V_1,V_2,V_3,他们对系统累计的噪声电压贡献是:
V_{total} = \sqrt{V_1^2 + V_2^2 + V_3^2}因此,如果一个噪声是其他噪声的数倍,那么这个噪声占主导地位。
单极点运算放大器
来看一个单极点运算放大器电路的噪声模型吧。在这个模型中,反馈网络是纯阻性(不包含电抗元件如电容、电感),且噪声增益与频率关系曲线平坦,是一个理想化的理论分析模型。
单极点运算放大器噪声模型
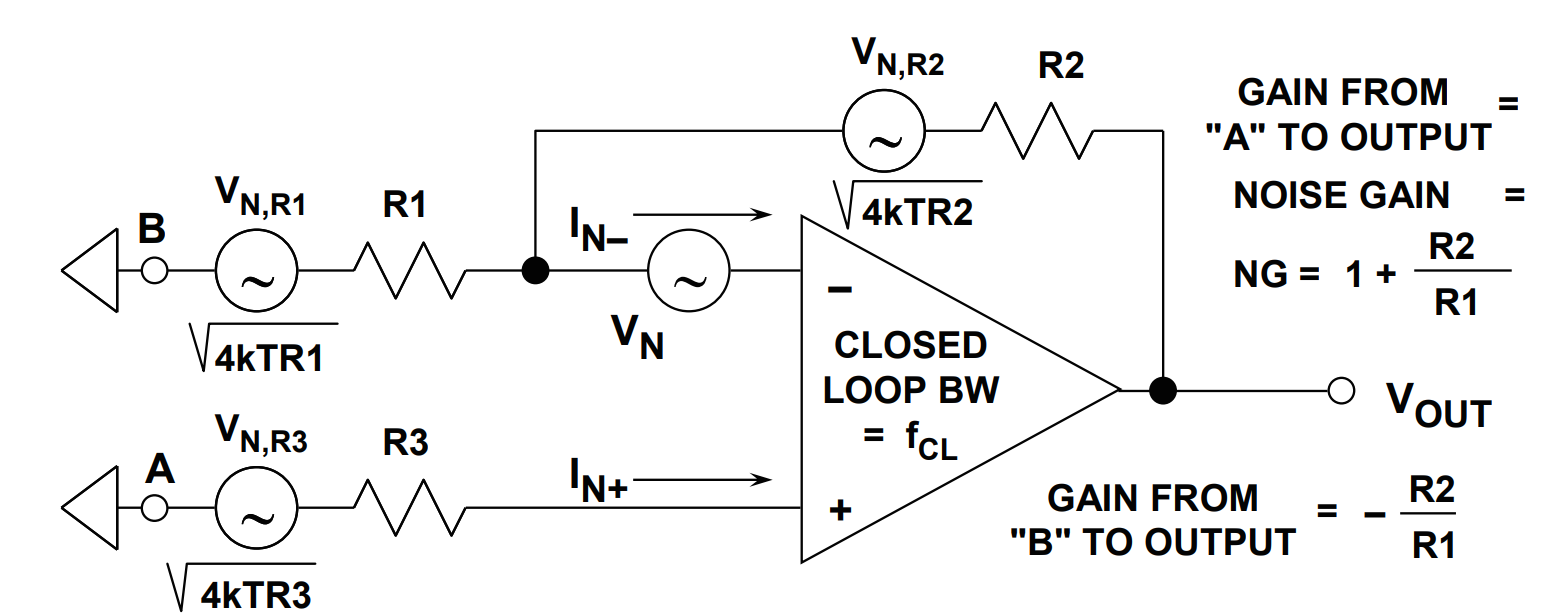
要计算一个放大电路的噪声性能,需要分别评估电路每一部分的噪声贡献,并确定以哪些噪声源为主导。为简化计算,在计算过程中不代入带宽,而是使用电压噪声谱密度来计算。
在上图所示的模型中有6个独立的噪声源:
- 3个电阻的约翰逊-奈奎斯特噪声(热噪声)
- OpAmp输入电压噪声
- OpAmp两端输入电流噪声
该电路从B节点到输出的增益为G,从A节点到输出的增益为噪声增益NG,分别如下:
G = -{R_2 \over R_1} \cdots 从A至输出\\
NG = 1 + {R_2 \over R_1} \cdots 从B至输出分析电路的增益和噪声源,可以得出如下各个独立噪声源的计算表格:
| 噪声源的电压噪声 | 折算到输出的增益因子 |
|---|---|
R3的热噪声:\sqrt{4kTR_3} |
NG = 1+{R_2 \over R_1} |
同相输入电流流入R3产生的电压噪声:I_{N_+}R_3 |
NG = 1+{R_2 \over R_1} |
输入电压噪声:V_N |
NG = 1+{R_2 \over R_1} |
R1的热噪声:\sqrt{4kTR_1} |
G = -{R_2 \over R_1} |
R2的热噪声:\sqrt{4kTR_2} |
1 |
反相输入电流流入R2产生的电压噪声:I_{N_-}R_2 |
1 |
然后将上述表格中的各个噪声源所贡献的电压噪声乘以其对应的增益因子,以方和根形式相加,再乘以计算噪声限定的带宽(BandWidth,BW),即可得到最终的噪声电压均方根值。(如果不乘以带宽,得到的是输出电压噪声谱密度)
V_{Noise} = \sqrt{BW} \cdot \sqrt{4kTR_3\cdot (1+{R_2\over R_1})^2 + (I_{N_+}R_3)^2\cdot (1+{R_2\over R_1})^2 + \\
V_N^2\cdot (1+{R_2\over R_1})^2 + 4kTR_1 \cdot {R_2^2 \over R_1^2} + 4kTR_2 + (I_{N_-}R_2)^2} \\
BW = 1.57\cdot f_{CL}其中,带宽BW等于1.57乘以运算放大器的闭环带宽f_{CL}。为什么要乘以1.57呢?
等效噪声带宽(ENB)
我们打断一下计算,中断进入这一小节,让我们看看什么是 等效噪声带宽(Equivalent Noise BandWidth)。
给定一个系统的传输函数 H(\jmath\omega),其等效噪声带宽定义为:
ENB = \Delta f = {1\over 2\pi} \int_0^\infty |{H(\jmath\omega) \over H(max)}|^2 d\omega其中,H(max)是传输函数 H(\jmath\omega)的最大值。看完这个数学公式云里雾里的,还是看图直观一些。

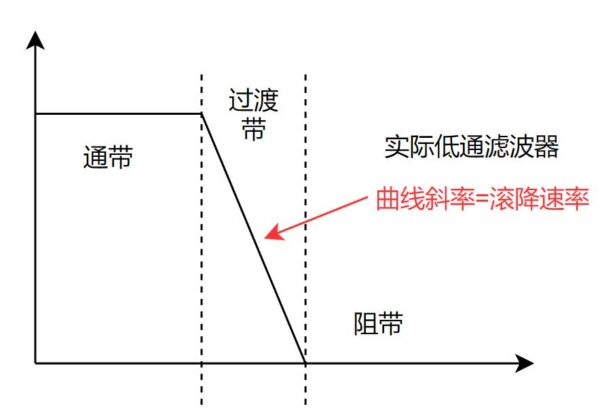
一个理想的滤波器的响应是 "砖墙式" 的,也就是在截止频率之前的所有频率信号无衰减地通过,截止频率之后的所有频率信号的衰减都是无穷大。从幅频特性曲线来看,它的响应就像一面墙,所以叫 "brickwall"。
而实际的滤波器是不可能具有砖墙式的响应的,一个低通滤波器的幅频特性曲线如实线所示,它在截止频率(-3dB频率)之后的增益是缓慢下降的。
现在我们构建一个虚拟的砖墙式滤波器B,让B的曲线所围成的面积和实际滤波器A的曲线在第一象限与坐标轴围成的面积相等,此时砖墙式滤波器的 \Delta f 的值,就是实际滤波器A的 等效噪声带宽(ENB)。
等效噪声带宽和实际滤波器截止频率 f_{3dB}的关系取决于 传输函数中的极点个数。一阶系统有一个极点,其换算系数为1.57。这就是之前我们分析的单极点运放噪声模型的噪声等效带宽和运放的闭环带宽之间的乘数关系咯。
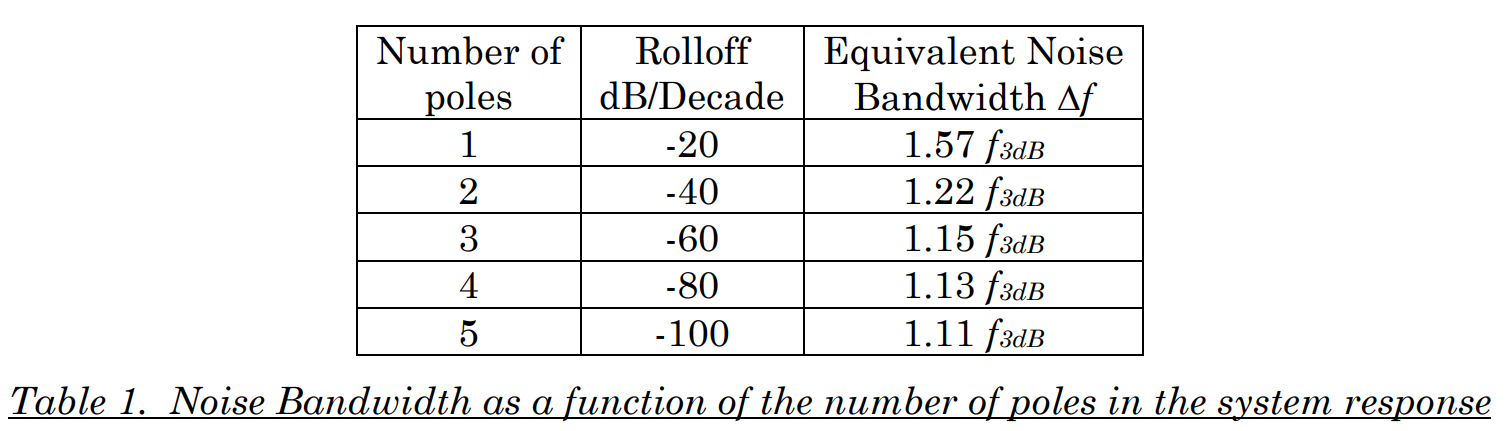
其实这个概念并不难理解。我们假设一个白噪声通过一个一阶低通滤波器,那么输出信号相比于输入将发生哪些变化呢?
- 如果低通滤波器是砖墙式响应,那么截止频率以上所有频率处的能量都为0;
- 如果低通滤波器不理想,即使是截止频率以上的频率分量仍存有残留能量;
将滤波器的非理想考虑进来,将"本应衰减完却未衰减"的高频成分能量积分,然后折合到低频处的平均能量水平并依此进行噪声带宽拓展,这样就可以得出等效噪声带宽。详细的数学推导与计算过程请参考附录Equivalent Noise Bandwidth。
噪声源贡献占比
回到我们的数学表达式上来。可以看到,选用不同的电阻值、不同的电路结构都会对运算放大器的总输出噪声造成影响。有时候运放自身的输入噪声占主导地位,有时又是电阻的热噪声占主导地位,有时又是电流噪声…选择不同的电阻组合和增益将会让噪声反复横跳,所以Be Careful, design with patience.
利用仿真工具对噪声进行仿真
单极点运算放大器的模型非常简单,看上去也便于计算。然而对于稍微复杂一点的电路,再想要手算噪声参数就困难多了。
好在我们有计算机辅助设计(CAD)工具。对于电路来说,spice是EE必不可少的趁手利器~。🐟用小巧强大的LTSpice搭建了一个仿真模型,对一个运算放大器的噪声进行仿真。
选用的运算放大器是Linear Technology生产的LT1028超低噪声运算放大器,其电压噪声密度典型值在1kHz时为 1nV/\sqrt{Hz},算得上是最顶级的低噪声运放之一了。
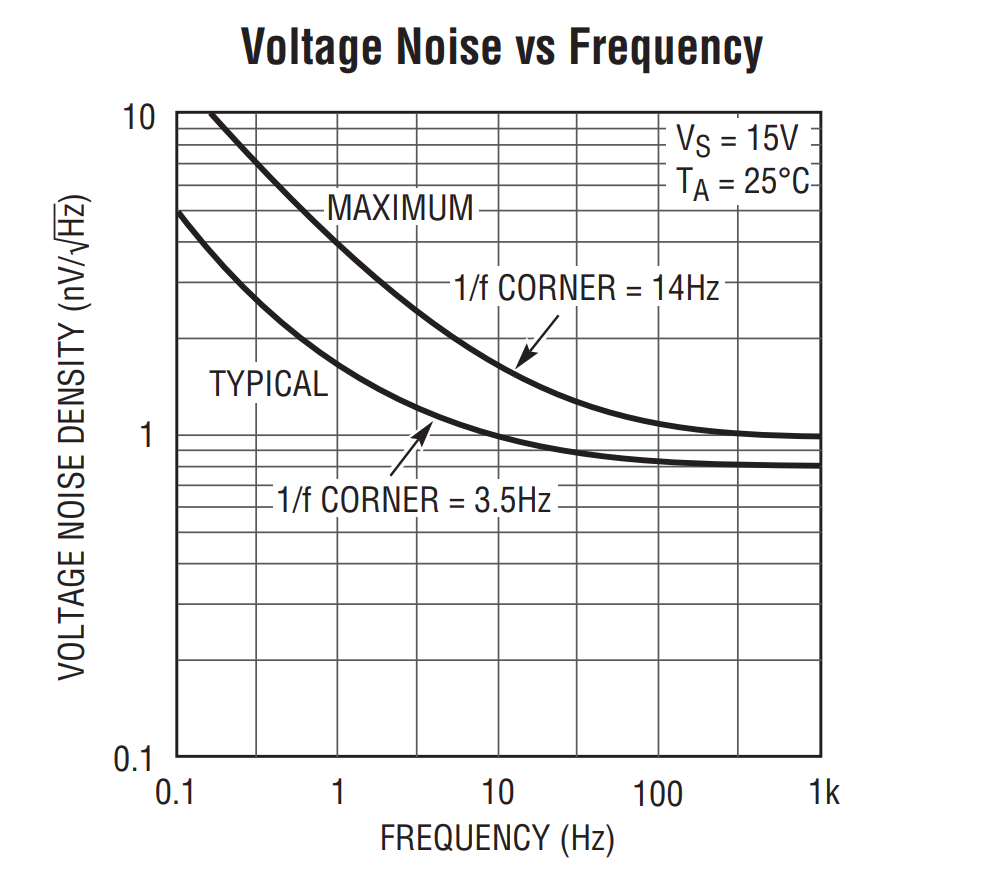
然后我搭建了一个增益为10(噪声增益为11)的反相放大器电路,电阻值故意选的hin大,就是为了引入更多的噪声XD
编辑仿真命令(Edit Simulation cmd),选择Noise分析,选择源和输出信号,配置扫描参数。
编辑完后,仿真语句会出现在schematic上,请注意输出源不能直接写标签名字,要用V()括起来,具体可以看我的电路图

运行仿真,点一下输出节点即可看到输出电压噪声密度曲线。可以看到,在此电路配置下,在1kHz-100kHz频段内的输出电压噪声密度达到了 116.7nV/\sqrt{Hz}。
鸭类鸭类,太大了。我们来减少一个噪声源,再看看输出噪声如何。把同相输入端的接地电阻R6咔了,再跑一次:

可以看到,咔掉这个电阻之后,噪声急剧下降,差不多减小了一半以上。让我们更进一步,维持电阻的比例不变(电路增益不变),将电阻阻值减小一些以减小热噪声,再跑一遍:
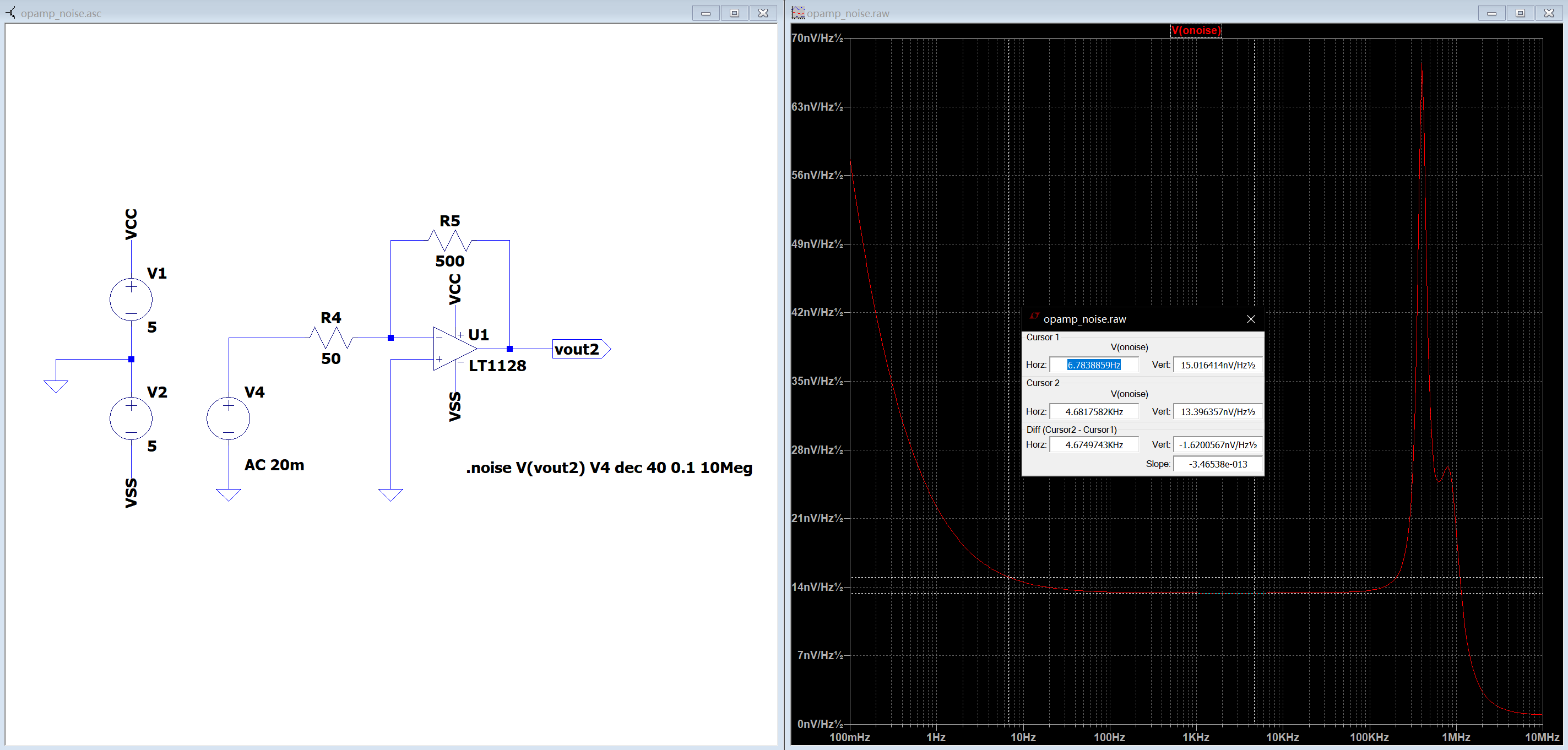
将电阻缩小了20倍,1kHz-100kHz频段内输出噪声谱密度直接降到了 14nV/\sqrt{Hz}的水准。如果除以电路增益10,折合输入噪声就是 1.4nV/\sqrt{Hz},仅仅比运算放大器自身的输入电压噪声密度高出一点点,现在才能较好发挥这颗低噪声运算放大器的性能了~
同时还有个小tip,按住ctrl键鼠标左键单击曲线图的标题(V(onoise)),可以得到在所展示的积分带宽内的电压噪声真有效值(相当于软件帮你把电压噪声谱密度对频率积分值给算出来咯)。
可以看到,针对上图的电路配置,该电路在0.1Hz至10MHz内的输出噪声真有效值为30.582uVrms,非常惊艳的性能。

同时我们注意到,不管我如何配置电路,输出电压噪声谱密度曲线总是在接近1MHz的地方有一个小尖峰。可以猜想到这可能是运放内部固有的某种结构所导致的噪声谱尖峰。如果我们对电路稍加修改,为其反馈支路并联一个电容,引入第二个极点,电路的噪声特性将如何改变呢?
其实这就是我尚未陈述的内容啦——二阶系统的运算放大器总输出噪声计算。其实没什么复杂的,在这里直接端出结果:除了运算放大器自身的输入电压噪声积分带宽不变外(如果同相输入端接有电阻,那么它的噪声和同相输入偏置电流噪声的积分带宽也不变),反相输入端的输入电阻、反馈电阻和反相输入电流噪声的积分带宽都取决于反馈电容与反馈电阻构成的低通截止点决定。
看一大段文字肯定晕了,直接看电路图吧~
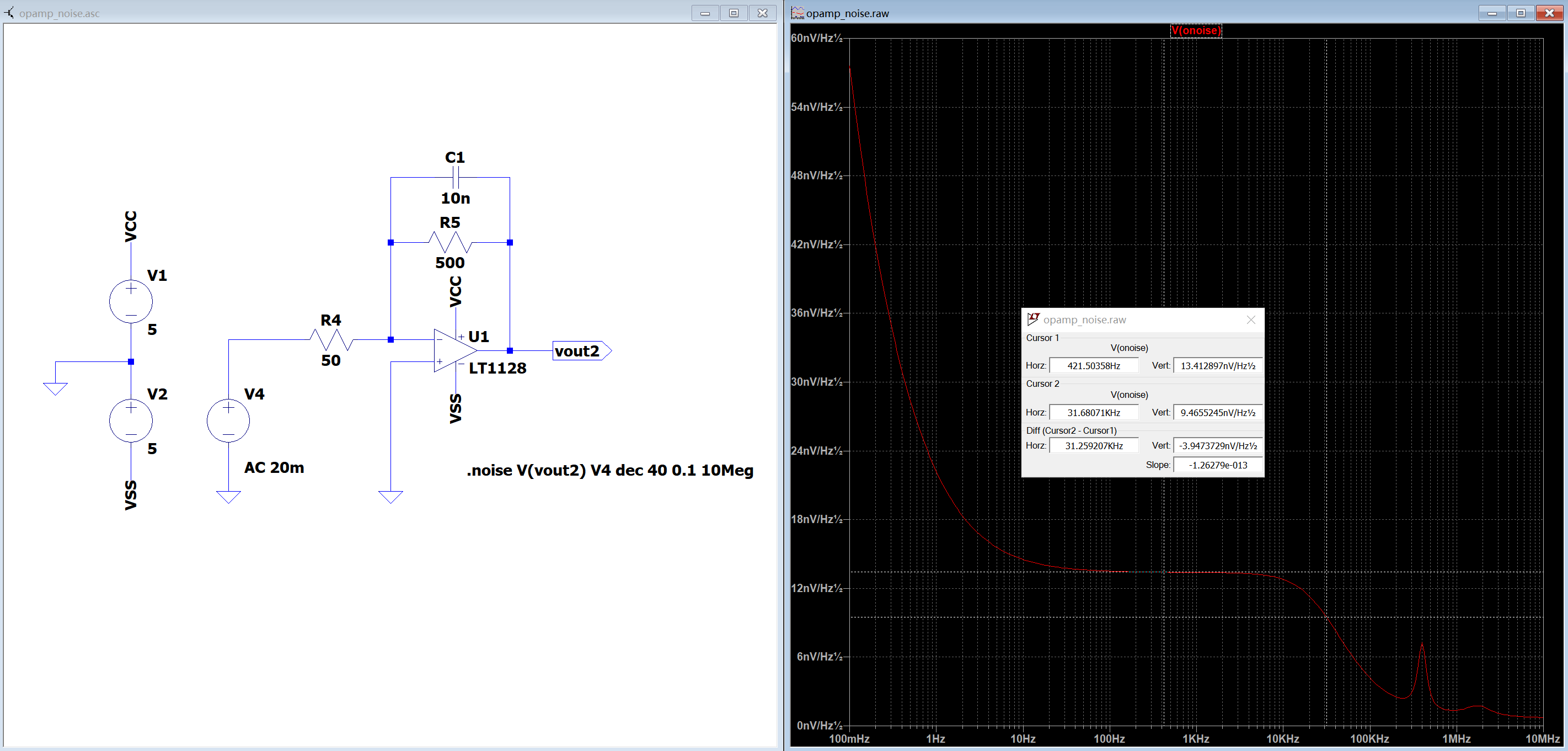
在500Ω反馈电阻上并联一个10nF电容,它们所构成的低通截止点为 {1\over 2\pi RC} = 31.83kHz。从输出电压噪声谱密度曲线中找到该频率点,同时与通带内的噪声电压密度所比较,其比值是0.707倍关系(-3dB),符合计算结果(无视极低频段的超越噪声哦)。
噪声的统计性质
我们常常有一个困惑,如何将电压的峰峰值与真有效值对应起来。但实际上它们并没有确定的换算公式,比如正弦波的真有效值是峰峰值除以0.707(2分之根号2),或者峰峰值是真有效值乘以1.414(根号2),但是这个换算关系对于其他的波形就很难适用了。
其背后的原因是,真有效值反映了信号能量的大小,如果想要精确计算一个周期信号的真有效值,在已知其数学表达式的情况下可以用积分的方式求解。但更多的信号是无规律可言的,即使采用傅里叶分析技术去测量真有效值,也难以做到高精度。真有效值测量又是一个大坑咯,不展开讲了,不然这篇文章又要拖更了…
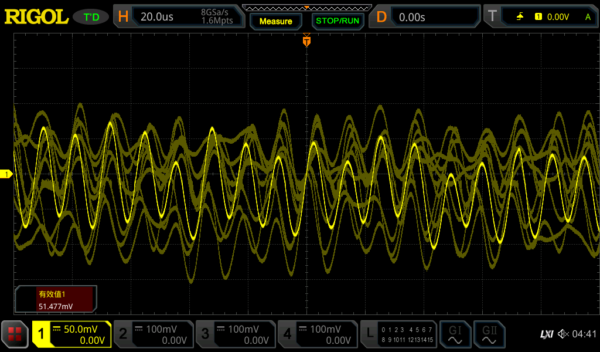
回到噪声信号,我们之前说白噪声是近似于高斯分布的。如果我们统计白噪声的瞬时幅度值并对其作直方图分析,会发现其瞬时幅度分布直方图是近似高斯分布的钟形曲线的。概率论与统计学告诉我们,对于给定真有效值的噪声信号,可以预测其瞬时幅度超过给定峰峰值的时间的百分比(也就是分布区间概率),如下表所示:

最常用的乘积因数是6.6,即电压噪声瞬时值99.9%的时间内不会超过6.6倍电压噪声真有效值(rms)。所以如果你测量到一个白噪声的峰峰值为6.6Vpp,那么它的真有效值大约就是1.0Vrms。