雷达信号处理-[1]-噪声信号与雷达基带信号产生

前言

这学期我和CNPP同学上了一门课，做了4个Matlab仿真实验，是关于雷达信号处理方面的，包括信号产生、加噪处理、滤波降噪处理、数字下变频解调、匹配滤波/脉冲压缩的内容。在此我们将实验报告稍作修改，扔到Emoe上，希望能帮到后来的童鞋们。

本系列将分为4篇，首尾相接发布。本文是第一篇，4篇的链接都在这里:

雷达信号处理-[1]-噪声信号与雷达基带信号产生
雷达信号处理-[2]-信号滤波与降噪
雷达信号处理-[3]-数字下变频(DDC)
雷达信号处理-[4]-匹配滤波与脉冲压缩

本系列文章的全部Matlab代码均放在github仓库中: RadarSignalProcessing_experiment

1.噪声信号的数学描述

1.1.均匀分布

f(x) = {1 \over {b-a}}, a < x < b \\
f(x) = 0, else

1.2.高斯分布

f(x)=\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(x-\mu)^2}{2\sigma^2})

1.3.瑞利分布

f(x)=\frac{x}{\sigma^2}exp(-\frac{x^2}{2\sigma^2}),x>0

1.4.复高斯噪声与瑞利分布的关系

设正弦波加窄带高斯噪声的混合信号为

r(t)=Acos({\omega}_c+\theta)+n(t)

式中：n(t)=n_c(t)cos\omega_ct-n_s(t)sin\omega_ct，为窄带高斯噪声，其均值为0，方差为\sigma^2_n；\theta为正弦波的随机相位，在(0,\ 2\pi)上均匀分布；振幅A和\omega_c均假定为确知量。于是：

r(t)=[Acos\theta+n_c(t)]cos\omega_ct-[Asin\theta+n_s(t)]sin\omega_ct \\
=z_c(t)cos\omega_ct+z_s(t)sin\omega_ct \\
=z(t)cos[\omega_ct+\phi(t)]

其中：

z_c(t)=Acos\theta+n_c(t) \\
z_c(t)=Asin\theta+n_s(t)

r(t)的包络和相位分别为：

z(t)=\sqrt{z_c^2(t)-z_s^2(t)},\ z\ge0 \\
\phi(t)=arctan\frac{z_s(t)}{z_c(t)}, \ 0{\le}z{\le}2\pi

考察r(t)的包络和相位的统计特性，如果\theta值已给定，则z_c、z_s是相互独立的高斯随机变量，且有：

E[z_c]=Acos\theta;\ E[z_s]=Asin\theta;\ \sigma_c^2=\sigma_s^2=\sigma_n^2

故在给定相位\theta的条件下z与\phi的联合概率密度函数为：

f(z_c,\ z_s/\theta)=\frac{1}{2\pi\sigma_n^2}exp\{-\frac{1}{2\sigma_n^2}[(z_c-Acos\theta)^2+(z_s-Asin\theta)^2]\}

根据z_c，z_s与z，\phi之间的随机变量关系：

z_c=zcos\phi;\ z_s=zsin\phi

可以求得在给定\theta的条件下z与\phi的联合概率密度函数为：

f(z_c,\ \phi/\theta)=f(z_c,\ z_s/\theta)\vert\frac{\partial(z_cz_s)}{\partial(z_s,\ \phi)}\vert=z{\cdot}f(z_c,\ z_s/\theta) \\
=\frac{z}{2\pi\sigma_n^2}exp\{-\frac{1}{2\sigma_n^2}[z^2+A^2-2Azcos(\theta-\phi)]\}

然后求给定\theta条件下的边际分布，即：

f(z/\theta)=\int_0^{2\pi}f(z_c,\ \phi/\theta)d\phi \\
=\frac{z}{2\pi\sigma_n^2}exp(-\frac{z^2+A^2}{2\sigma_n^2})\cdot\int_0^{2\pi}exp[\frac{Az}{\sigma_n^2}cos(\theta-\phi)]
d\phi

由于：

\frac{1}{2\pi}\int_0^{2\pi}exp[xcos\phi]d\phi=I_0(x)

故有：

\frac{1}{2\pi}\int_0^{2\pi}exp[\frac{Az}{\sigma_n^2}cos(\theta-\phi)]d\phi=I_0(\frac{Az}{\sigma_n^2})

式中：I_0(x)为第一类零阶修正贝塞尔函数。

当x\ge0时，I_0(x)是单调上升函数，且有I_0(0)=1，因此：

f(z/\theta)=\frac{z}{\sigma_n^2}exp(-\frac{z^2+A^2}{2\sigma_n^2}){\cdot}I_0(\frac{A_z}{\sigma_n^2})

由上式可见，f(z/\theta)与\theta无关，故r(t)的包络z的概率密度函数为

f(z)=\frac{z}{\sigma_n^2}exp(-\frac{z^2+A^2}{2\sigma_n^2}){\cdot}I_0(\frac{A_z}{\sigma_n^2}),\ z\ge0

此概率密度函数称为广义瑞利分布，又称莱斯分布。其存在两种极限情况：

1. 当信号很小，即A\to0时，信号功率与噪声的比值\gamma=\frac{A^2}{2\theta_n^2}\to0，相当于x很小，于是有I_0(x)=1，莱斯分布退化为瑞利分布；

f(z)\approx\frac{z}{\sigma_n^2}exp(-\frac{z^2}{2\sigma_n^2}),\ z\ge0

1. 当信噪比\gamma=\frac{A^2}{2\theta_n^2}很大时，有I_0(x)\approx\frac{e^x}{\sqrt{2{\pi}x}}，这时在z{\approx}A附近，f(z)近似为高斯分布，即：

f(z)\approx\frac{1}{\sqrt{2\pi}\sigma_n}exp(-\frac{(z-A)^2}{2\sigma_n^2})

2.噪声信号产生

均匀分布噪声产生（matlab代码）

可见其时域波形图、直方图、频谱图。可以看到其直方图呈现出均匀分布的特征，在其频带内各频点能量分布均匀，符合白噪声特性

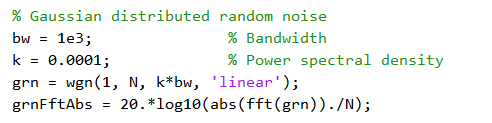
高斯分布噪声产生（matlab代码）

可见其时域波形图、直方图、频谱图。可以看到其直方图呈现出高斯钟形曲线特征，在其频带内各频点能量分布均匀，符合白噪声特性

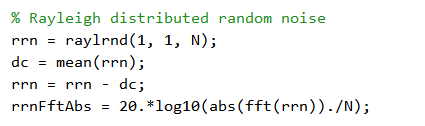
瑞利分布噪声产生（matlab代码）

可见其时域波形图、直方图、频谱图。可以看到其直方图呈现出瑞利分布特征，在其频带内各频点能量分布均匀，符合白噪声特性

3.雷达信号产生与加噪

3.1 BPSK信号产生与加噪

matlab代码如下，码元为1101010001

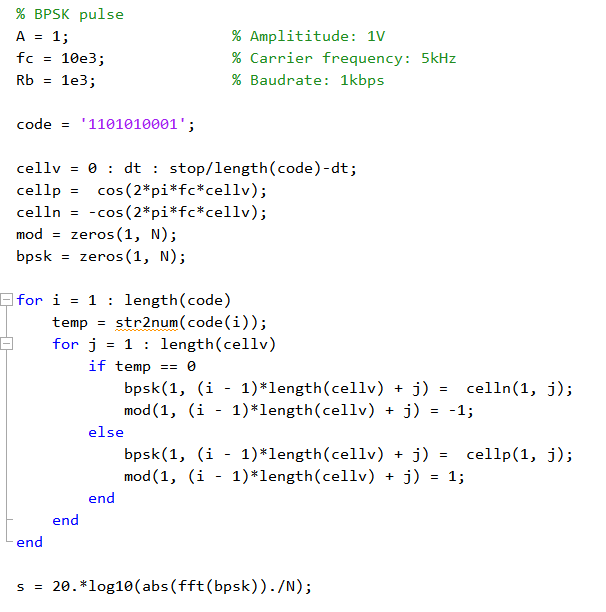
产生的BPSK码元信号、调制后信号以及调制后信号的频谱

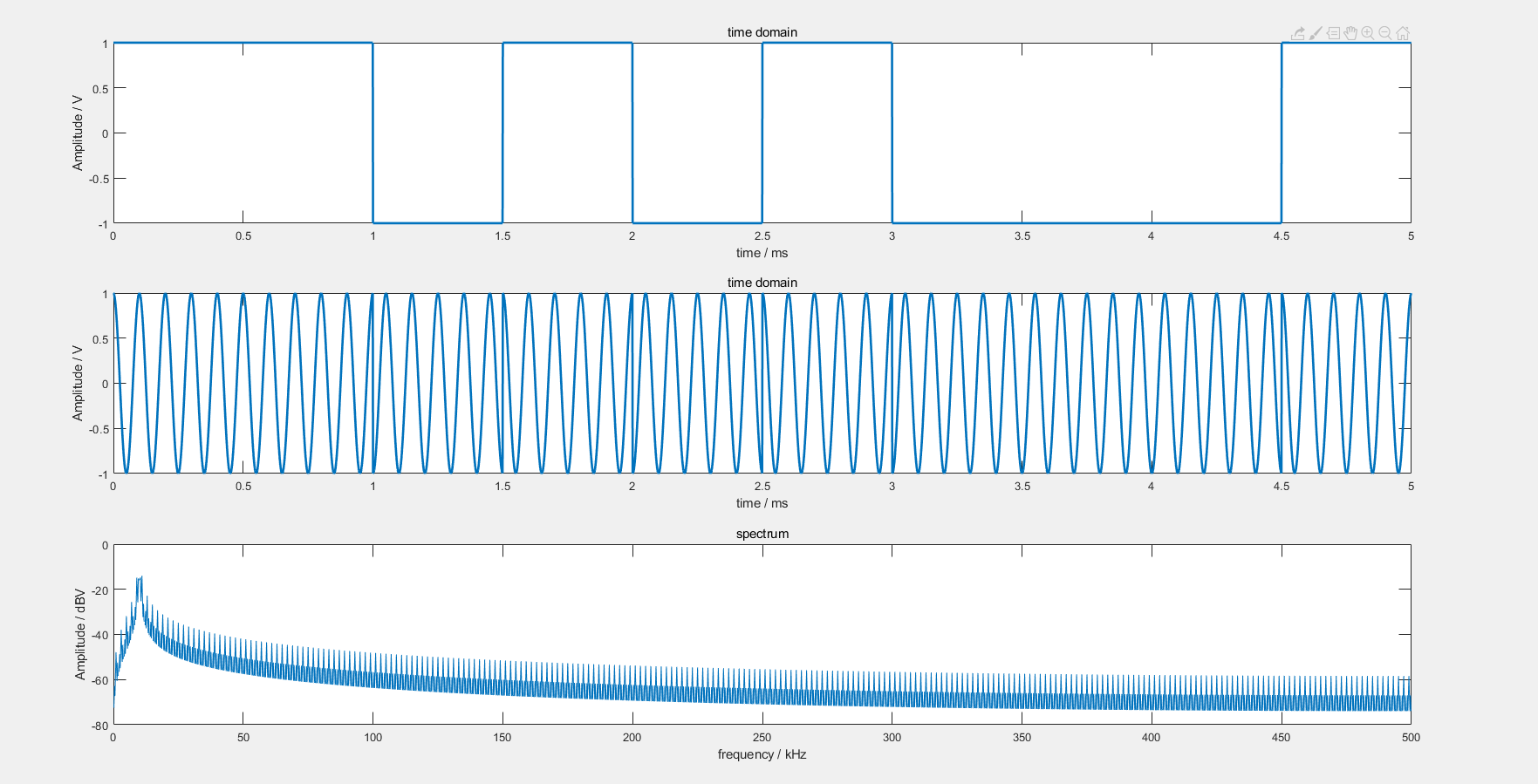
可以看出其频谱有明显的谐波特性，因其原始信号为正弦与方波相乘，频域相乘时域卷积，方波的谐波成分反映到了调制后信号的频谱中。

现在对BPSK调制信号添加噪声。可明显看出其时域波形上的毛刺与尖峰。

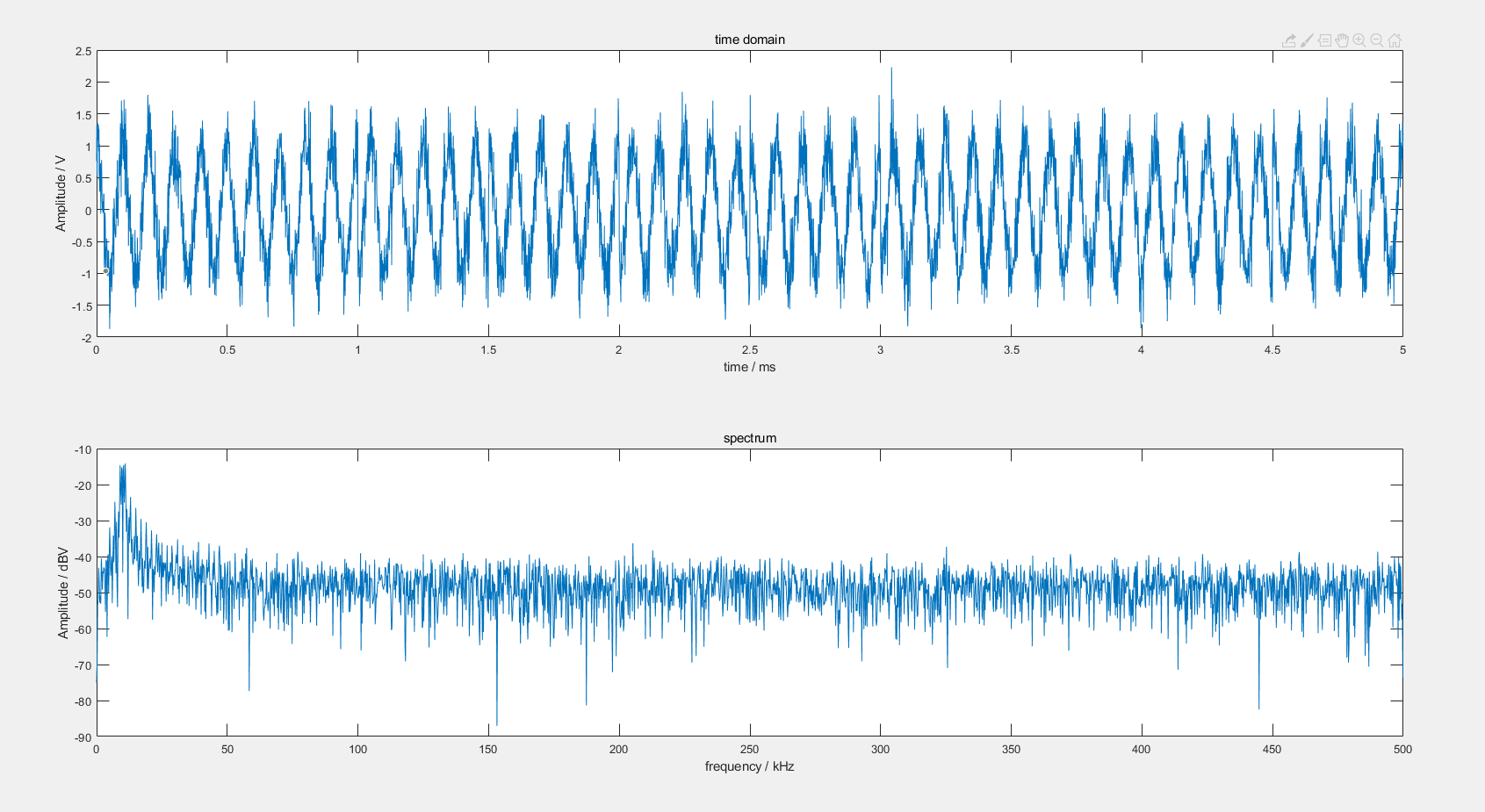
3.2 LFM（Linear Frequency Modulation）信号产生与加噪

matlab代码如下

产生的LFM信号波形，以及其调制波形，能谱图和频谱图

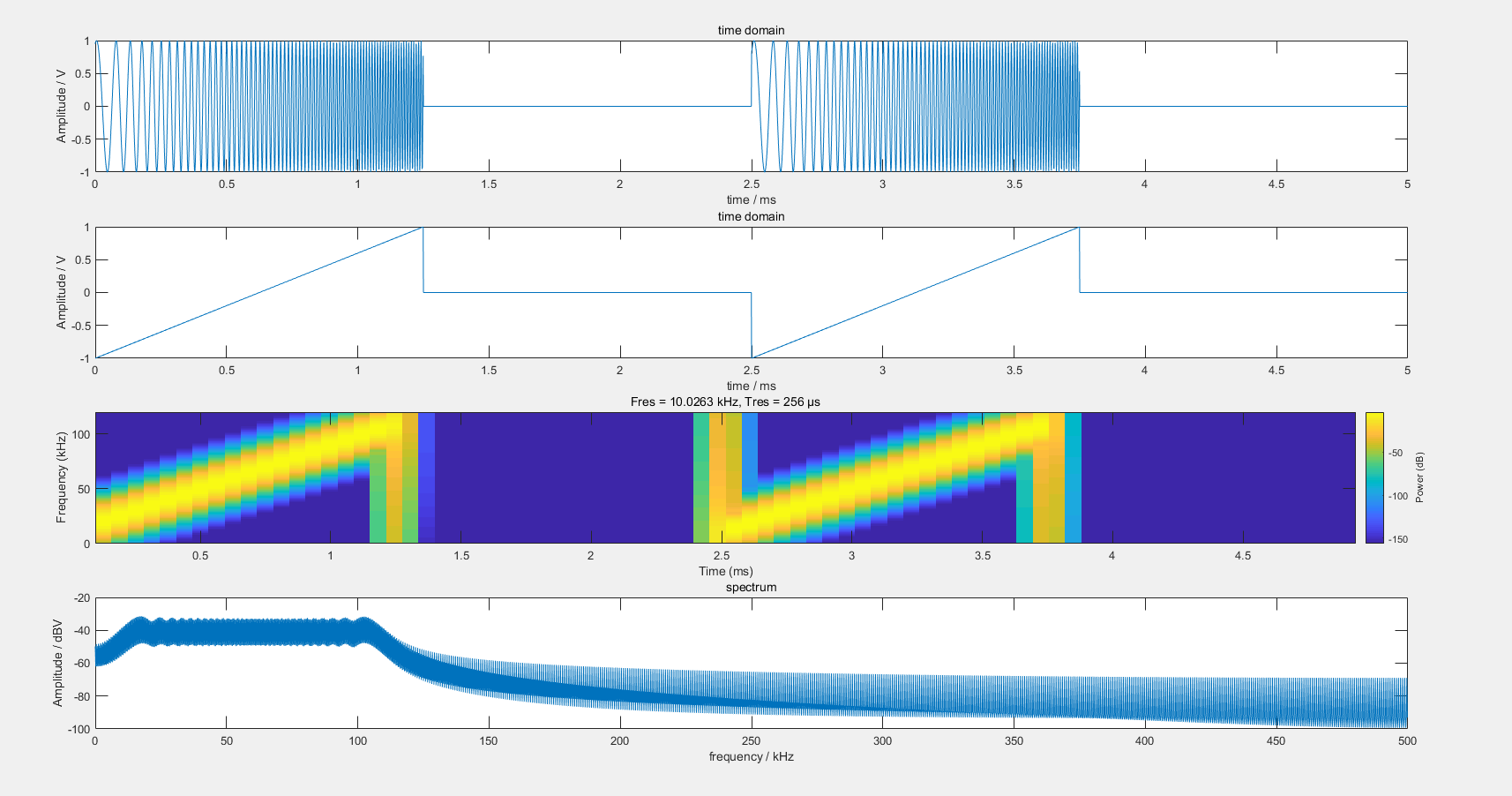
可以看出其频谱也具有明显的谐波特性，因其原始信号为正弦与带斜率的线性波相乘，同时带有突变成分，突变成分意味着具有高频谐波，该谐波成分反映到了调制后信号的频谱中。

现在对LFM调制信号添加噪声。可明显看出其时域波形上的毛刺与尖峰。

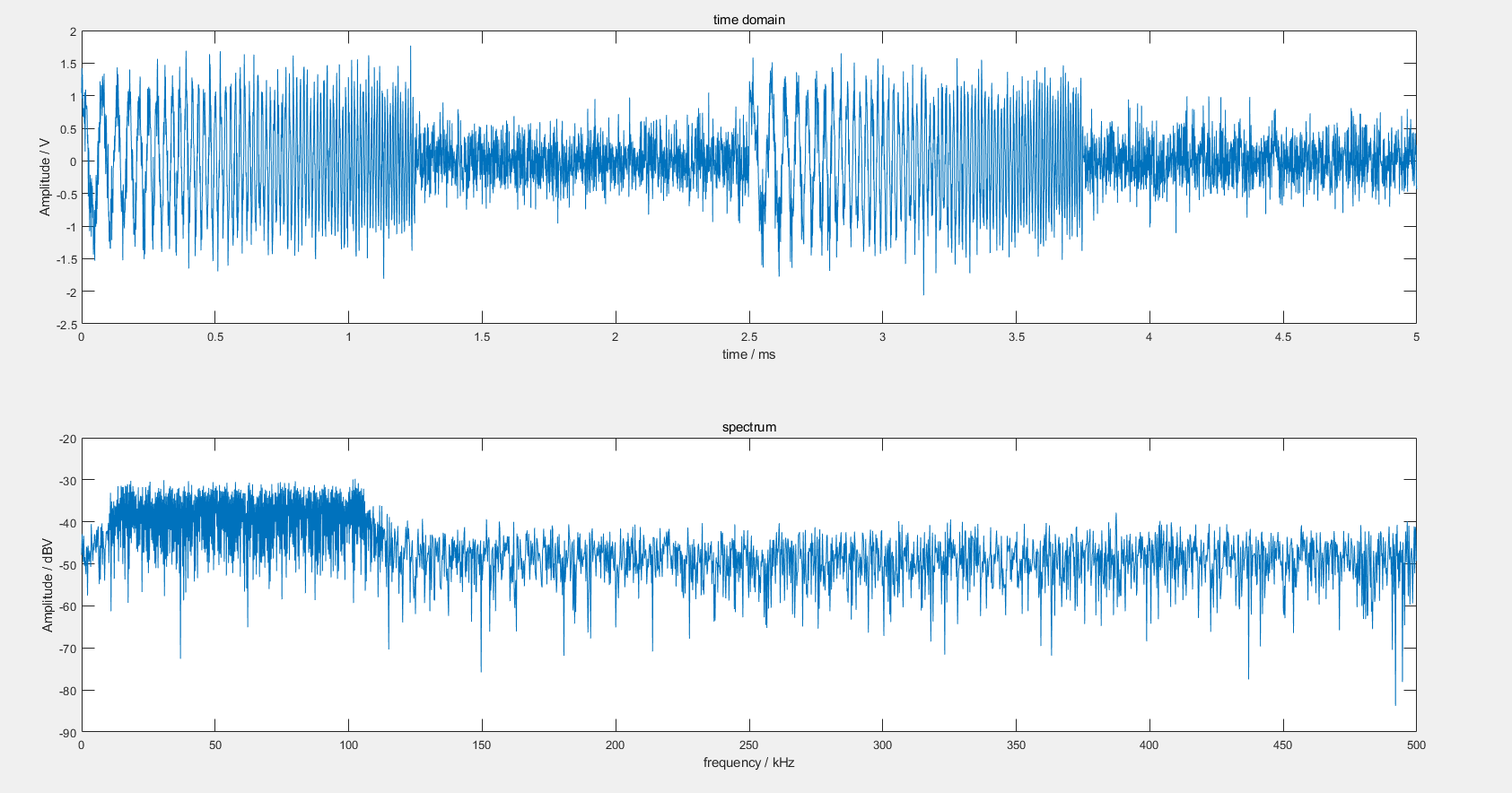
4. LFM信号 HDL实现

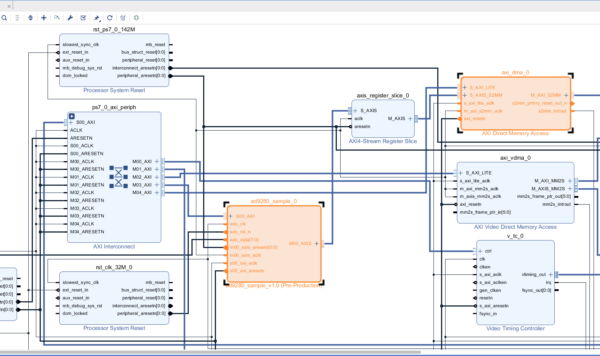
使用Verilog HDL硬件描述语言编写LFM信号产生的仿真实验，系统框图如下:

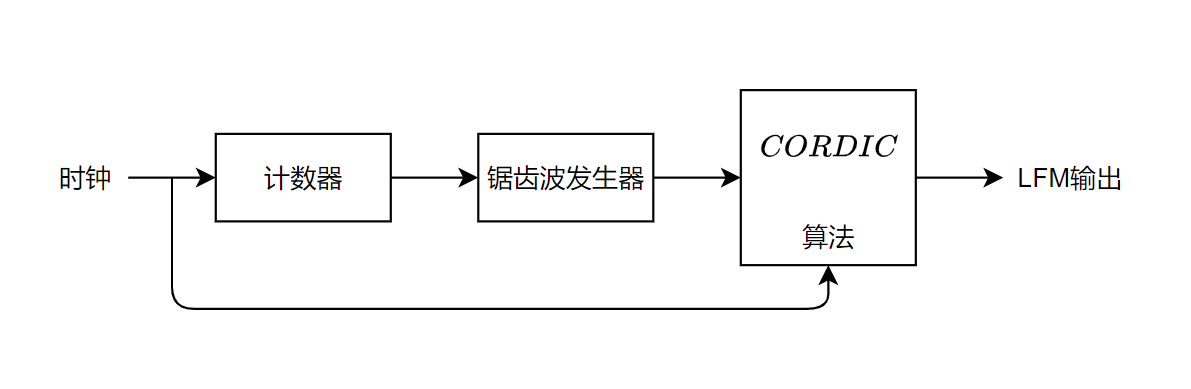
利用Cordic算法进行单周期快速正弦运算可以大幅提升正余弦计算速度。使用锯齿波作为控制信号，对VCO正弦进行调制即可得到LFM信号，仿真波形图如下:

可以看到LFM信号产生效果极佳。

5. 参考

轻松搞懂均匀分布、高斯分布、瑞利分布、莱斯分布（含MATLAB代码）

Matlab仿真产生复高斯白噪声，验证包络服从瑞利分布，包络平方服从指数分布

matlab中生成瑞利信道的两种方法

BPSK基带调制系统MATLAB仿真实现(1)